NeurIPS-2019 论文整理

NeurIPS-2019 还在审稿中，但是很多文章已经在ArXiv上release出来了，本文记录一些最近看过的NeurIPS文章

Machine learning

When Does Label Smoothing Help?

Hinton组有关label smoothing和distillation的新文章，文章总体偏实验，empirical results有以下几点发现：

作者提出了一种新的神经网络可视化方法，将神经网络倒数第二层的神经元输出进行可视化后，发现加了label smoothing的model类内间距要比不加label smoothing的小
label smoothing implicitly calibrates learned models so that the confidences of their predictions are more aligned with the accuracies of their predictions.
label smoothing在缩小类内间距，降低不同类别的耦合程度的同时，从而提高网络的准确性，也抹消掉了类间的的一些semantic information，所以做distillation的时候，teacher网络用加了label smoothing的反而比不加的更差，i.e., teacher网络的acc高不是student蒸馏效果好的充分条件

下图是1的实验

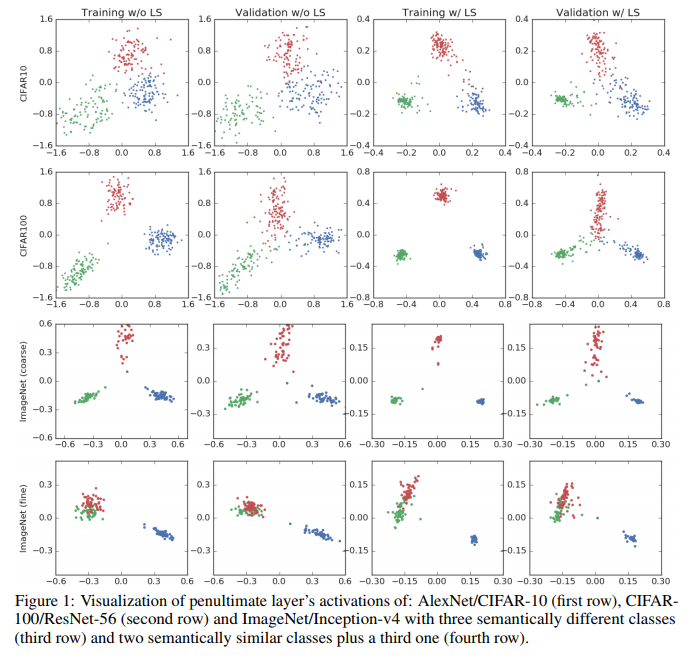
2的实验（个人感觉结果没有很significant，不过实验的setting上确实挑不出刺来）

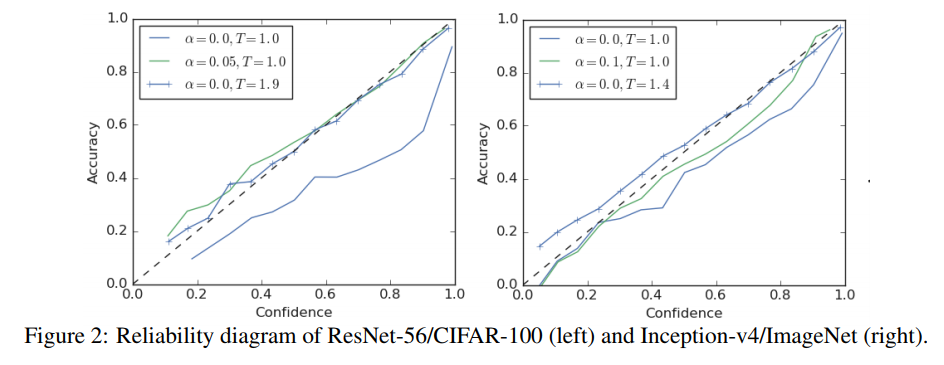
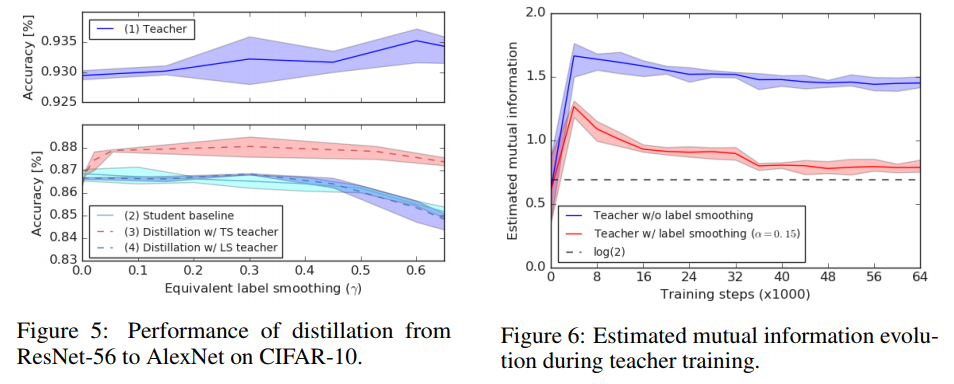
为了说明结论3，作者用一些近似的方法可视化了输入样本与倒数第二层的softmax logits之间的互信息，发现加了label smoothing的teacher互信息比不加label smoothing的要低很多，因此得出结论

The figure shows that using these better performing teachers is no better, and sometimes worse, than training the student directly with label smoothing, as the relative information between logits is “erased” when the teacher is trained with label smoothing.

Therefore, a teacher with better accuracy is not necessarily the one that distills better.

You Only Propagate Once: Accelerating Adversarial Training via Maximal Principle

大佬Yiping Lu的文章，题目模仿了YOLO的风格，主要解决的问题是加速基于PGD的adversarial training过程

对抗攻击问题可以写作

$\min_{\theta}\max_{\eta\leq{\epsilon}}\mathbb{E}_{x}[J(x+\eta,y;\theta)]$

可以看出主要的计算量瓶颈在于内层循环的maximization，作者的方法是通过chain rule分解，近似认为 adversarial perturbation $\eta$ 只与神经网络第一层有关，假设n层的神经网络映射表示为

$J(f_{n}(\dots f(f_{2}(f_{1}(f_{0}(x+\eta,\theta_{0}),\theta_{1}),\theta_{2}),\dots,\theta_{n}))$

则 $\nabla_{\eta}J(.)=\nabla_{f_{0}}J(.)\nabla_{\eta}f(x+\eta,\theta_{0})$，作者的思路是fix前面一项，认为 $p=\nabla_{f_{0}}J(.)$，在inner loop中只算一次 $p$ ，剩余时间都只back-propagate第一层，由此减少PGD的计算量

显然这是一种approximation，因为网络后面的层的响应是会受到前面 $x+\eta$ 影响的，那么问题就来了

这种approximation是否有bound？
这种优化得到的最优解是否唯一？
这种优化是否可以收敛？

作者在theorem 1中证明：如果将神经网络每层的映射看成一个离散ode，定义Hamiltonian为

$H_{t}(x,p,\theta_{t})=pf_{t}(x,\theta_{t})-\frac{1}{B}R_{t}(x,\theta_{t})$

那么只有第一层会包含 $\eta$ 项，满足性质

因此这种优化方式存在最优解

文章证明涉及 Pontryagin’s Maximum Principal ，这里的背景不是很懂
Theorem 1中 $\{ f_{t}(x,\theta):\theta\in{\Theta} \}$ convex w.r.t. $t$ ，这个条件在实际应用中ResNet是否满足？

Reinforcement learning

Imitation learning without interacting with environment

出自NeurIPS 2018的文章Exponentially Weighted Imitation Learning for Batched Historical Data，由AILab独立完成，作者列表里Han Liu与前主任Tong Zhang榜上有名

文章研究的背景非常贴合我们的业务，目前主流的imitation learning方法，无论是早期的DAgger还是后来的各种GAIL类方法，训练的过程中都必须要和environment做交互，然而实践中很多情况下与环境交互的成本是非常高的，举几个例子

OpenAI的Dota2，DeepMind的AlphaGo系列，一个是不完全信息的多智体博弈，一个是完全信息的MCTS模拟，采用的与环境交互方式都是self-play，因此不需要任何人类数据，agent可以真正意义上做到在与environment的交互中学习——为此付出的代价是学习过程非常的漫长，无论是OpenAI还是DeepMind都需要相当于人类上万年的学习时间来达到一个能看得过去的结果
Robotics领域中，现实场景下做交互不能像在simulator里一样随心所欲，机械臂还是很容易坏掉的，以往robotics的人经常考虑的是用model-based learning方法进行学习，然而model-based的方法在复杂环境、大型MDP下复杂度极高

这篇文章的background setting如题所述：我们只有batched historical data，而不能用任何方法与environment做直接交互

Q1: How about directly train a policy model with supervised learning (behavior cloning)?

首先一个显而易见的问题在于distributional shift，其次我们的historical batched data中，每个state都会对应一个reward，这是reinforcement learning与supervised learning的一个重大的差异

If we can not make full use of the reward signal in data, the performance of behavior cloning will certainly be upper bouned by the batched historical data.

This paper tries to address the problem of learning a better policy than the expert policy with only batched historical data.

Algorithm and analysis

算法本身非常简单，具体实现时除了policy network $\pi_{\theta}$，我们还需要用supervised learning训练一个$V_{w}(s_{t})$，之前的paper中一般的做法是用cumulated reward $R_{t}$ 算: $A(s_{t},a_{t})=\mathbb{E}_{\pi}[R_{t}-V_{w}(s_{t})]$，文中作者表示他们的做法是$A(s_{t},a_{t})=(R_{t}-V_{w}(s_{t}))/c$, where $c$ is the exponential moving average norm of the advantage, to make the scale of $\beta$ stable across different environments，这种做法计算复杂度也相对较低

这段分析在看的时候就很头大，看rebuttal记录时发现reviewer和我提出了类似的疑问，主要有两点

Regarding the state distribution $d(s)$, I assume it is always referring to the state distribution of the behavior policy $\pi$. However, below line 146, when you say that it is imitating a new hypothetic policy $\tilde{\pi}$, shouldn’t the state distribution becomes the state-distribution resulting from $\tilde{\pi}$? The state distribution of $\tilde{\pi}$ and $\pi$ could be different.

我暂时没证出来$d^{\tilde{\pi}}(s)\propto{d^{\pi}(s)\exp(-C(s))}$